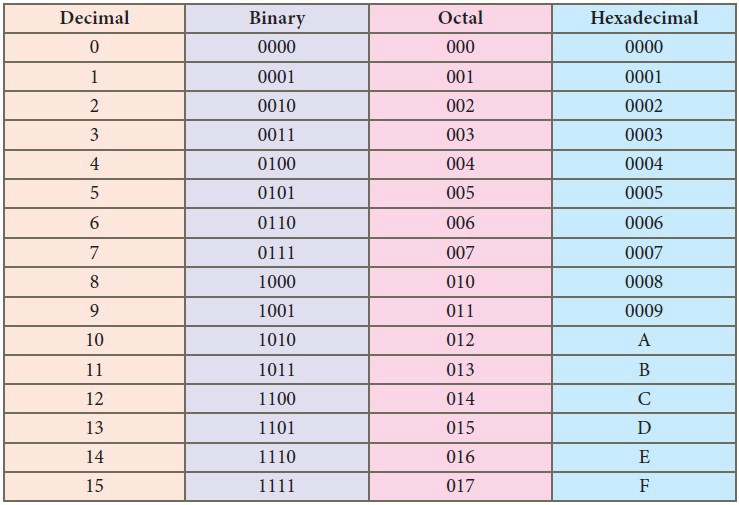
Sayı Sistemleri, Çocukluğumuzdan beri hepimiz rakamlarla az çok haşır neşiriz.
Peki, kullandığımız ondalık sayı sisteminden başka sayı sistemleri olduğunu biliyor muydunuz?
Sayı Sistemi Nedir?
Sayı sistemleri, sayıları adlandırma ve temsil etmeye yarar. Hepimiz genel olarak ondalık sayı sitemine aşinayız fakat çoğu kişi ikili, sekizli ve on altılı sayı sistemlerini bilmiyor.
Yaygın Olarak Kullanılan Sayı Sistemleri
*Ondalık Sayı Sistemi (Decimal Number System) – Hepimizin bildiği gibi, bu sistem herhangi bir sayıyı temsil etmek için 0 ila 9 arasında 10 basamak kullanır.
*İkili Sayı Sistemi (Binary Number System) – Bu sistem, sayı gösterimi için 0 ve 1 olan 2 basamak kullanır.
Örneğin, ondalık sayıdaki 10 sayısı ikili sayı sisteminde 1010 olarak gösterilir.
*Sekizli Sayı Sistemi (Octal Number System) – Bu sistem sayı gösterimi için 0 ile 8 arasında 8 basamak kullanır.
Örneğin, ondalık sayı sistemindeki 9, sekizlik sayı sisteminde 11 olarak gösterilir.
*On altılı Sayı Sistemi (Hexadecimal Number System) – Bu sistem, sayı gösterimi için 0 ila 10 ve A ila F (EVET! Sayıların içinde harfler) olan 16 basamak kullanır.
Örneğin, ondalık sayı sistemindeki 30 sayısı onaltılık sistemde 1E olarak gösterilir.
Sayıların Dönüşümü
Başka bir sayı sistemindeki bir sayıyı nasıl okuruz?
Farklı sistemden bir sayıyı okurken, şimdiye kadar kullandığımız onluk sayı sistemi üzerinden düşünerek okuruz.
Şimdi ondalık sayı sistemini nasıl öğrendiysek diğerlerini de o şekilde öğrenelim.
9.05.000 gibi bir sayıyı nasıl okuruz?
En sağdaki basamaktan başlıyoruz ve taban değerini 1 olarak alıyoruz ve her bir basamak sola kaydığımızda, taban değerini bir önceki taban değerinin 10 katı olarak alıyoruz, değil mi?
Ve sonunda tüm rakamların çarpımlarını kendi temel değerleriyle çarpıyoruz.
Aslında diğer sistemler de bu mantıkla çalışır.
İnceleyelim:
İkili Sayı Sistemi (Binary Number System)
İkili sayımızı 101010 olarak alalım.

Sayıyı ondalık sisteme dönüştürmek için en sağdaki basamaktan başlıyoruz.
Yukarıdaki görselde her basamağın temel değerini görebiliriz. Bu sefer sola doğru kayarken taban değerini 2’nin katları olarak alıyoruz.
Böylece ikili sayımız her bir basamağın taban değeri kullanılarak ondalık sayı sistemine dönüştürülebilir, karşılık gelen basamakla çarpılır ve hepsi toplanır:
( 0 x 2⁰ ) +(1 x 2¹) +( 0 x 2²) +(1 x 2³) +( 0 x 2⁴) +(1 x 2⁵) = 42
On altılı Sayı Sistemi (Hexadecimal Number System)
On altılı sayımızı 5C8A olarak alalım.
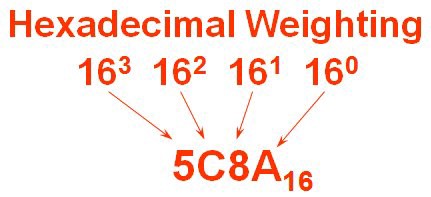
Yine aynı şekilde başlıyoruz ve bu kez sola doğru kayarken taban değerini 16’nın katları olarak alıyoruz. Buradaki fark ise harfleri de kullanıyor olmamızdır.
Harfleri 9’dan sonraki sayılar olarak düşünüyoruz. A-10, B-11, C-12, D-13, E-14, F-15 gibi.
Şimdi Hesaplayalım:
( 10 x 16⁰ ) + ( 8 x 16¹ ) +( 12 x 16² ) +( 5 x 16³ ) = 23690
Diğer sayı sistemleri de aynı şekilde çevrilir.
Neden Farklı Sayı Sistemleri Var?
Çünkü her uygulamaya sadece bir sayı sistemi koyamayız. Hepimiz ondalık sayı sistemine çok aşinayız ve bu sistemi kullanarak işlem yapmaktan çok memnunuz. Ancak bazı uygulamalar ve verimli programlar için farklı sistemler kullanmamız gerekiyor.
*İkili Sistem – Bilgisayarlarda ikili dili kullanıyoruz. Bir bilgisayar yalnızca 0 ve 1 sayılarını (ikili sayıları) anlar. Bilgisayarda yazdığınız, okuduğunuz, sakladığınız veya herhangi bir işlem yaptığınız, en temel düzeyde, bilgisayar tarafından 0’lar ve 1’ler dizisi olarak işlenir. İkili sistem kullanmak, hesaplamaları basit tutmaya ve gerekli devre miktarını daha az tutmaya yardımcı olur, bu da en az yer, enerji tüketimi ve maliyetle sonuçlanır.
*Onaltılı sistem – Onaltılı sayı sistemi, programcılar tarafından genellikle ikili sayı sistemini basitleştirmek için kullanılır. Onaltılık numaralandırmanın kullanımını, bellekte konumların tanımlanması, renklerin depolanması (her birinin onaltılık basamak olduğu #RRGGBB), MAC adreslemesi, IPv6 adreslemesi yerleri örnek olarak gösterebiliriz.



